[Note: This post is part of a set of three where thoughts related to my job leaked into the blog. They don't really fit with the surrounding posts; you may want to skip them.]
1
Choice is a crucial component of reasoning. Given a set of available actions, which action do you take? Do you go out to the movies or stay in with a book? Do you capture the bishop or fork the king? Somehow, we must reason about our options and choose the best one.
Of course, we humans don't consciously weigh all of our actions. Many of our choices are made subconsciously. (Which letter will I type next? When will I get a drink of water?) Yet even if the choices are made by subconscious heuristics, they must be made somehow.
In practice, decisions are often made on autopilot. We don't weigh every available alternative when it's time to prepare for work in the morning, we just pattern-match the situation and carry out some routine. This is a shortcut that saves time and cognitive energy. Yet, no matter how much we stick to routines, we still spend some of our time making hard choices, weighing alternatives, and predicting which available action will serve us best.
The study of how to make these sorts of decisions is known as Decision Theory. This field of research is closely intertwined with Economics, Philosophy, Mathematics, and (of course) Game Theory. It will be the subject of today's post.
2
Decisions about what action to choose necessarily involve counterfactual reasoning, in the sense that we reason about what would happen if we took actions which we (in fact) will not take.
We all have some way of performing this counterfactual reasoning. Most of us can visualize what would happen if we did something that we aren't going to do. For example, consider shouting "PUPPIES!" at the top of your lungs right now. I bet you won't do it, but I also bet that you can picture the results.
One of the major goals of decision theory is to formalize this counterfactual reasoning: if we had unlimited resources then how would we compute alternatives so as to ensure that we always pick the best possible action? This question is harder than it looks, for reasons explored below: counterfactal reasoning can encounter many pitfalls.
A second major goal of decision theory is this: human counterfactual reasoning sometimes runs afoul of those pitfalls, and a formal understanding of decision theory can help humans make better decisions. It's no coincidence that Game Theory was developed during the cold war!
(My major goal in decision theory is to understand it as part of the process of learning how to construct a machine intelligence that reliably reasons well. This provides the motivation to nitpick existing decision theories. If they're broken then we had better learn that sooner rather than later.)
3
Sometimes, it's easy to choose the best available action. You consider each action in turn, and predict the outcome, and then pick the action that leads to the best outcome. This can be difficult when accurate predictions are unavailable, but that's not the problem that we address with decision theory. The problem we address is that sometimes it is difficult to reason about what would happen if you took a given action.
For example, imagine that you know of a fortune teller who can reliably read palms to divine destinies. Most people who get a good fortune wind up happy, while most people who get a bad fortune wind up sad. It's been experimentally verified that she can use information on palms to reliably make inferences about the palm-owner's destiny.
So... should you get palm surgery to change your fate?
If you're bad at reasoning about counterfactuals, you might reason as follows:
Nine out of ten people who get a good fortune do well in life. I had better use the palm surgery to ensure a good fortune!
Now admittedly, if palm reading is shown to work, the first thing you should do is check whether you can alter destiny by altering your palms. However, assuming that changing your palm doesn't drastically affect your fate, this sort of reasoning is quite silly.
The above reasoning process conflates correlation with causal control. The above reasoner gets palm surgery because they want a good destiny. But while your palm may give information about their destiny, your palm does not control your fate.
If we find out that we've been using this sort of reasoning, we can usually do better by considering actions only on the basis of what they cause.
4
This idea leads us to causal decision theory (CDT), which demands that we consider actions based only upon the causal effects of those actions.
Actions are considered using causal counterfactual reasoning. Though causal counterfactual reasoning can be formalized in many ways, we will consider graphical models specifically. Roughly, a causal graph is a graph where the world model is divided into a series of nodes, with arrows signifying the causal connections between the nodes. For a more formal introduction, you'll need to consult a textbook. As an example, here's a causal graph for the palm-reading scenario above:
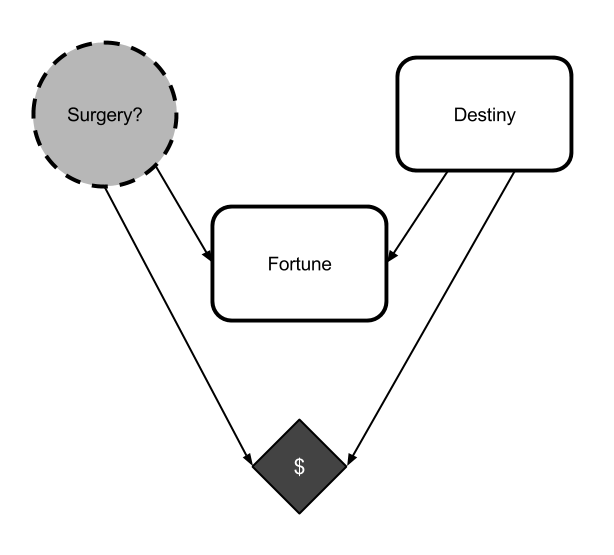
The choice is denoted by the dotted Surgery? node. Your payoff is the $ diamond. Each node is specified as a function of all nodes causing it.
For example, in a very simple deterministic version of the palm-reading scenario, the nodes could be specified as follows:
Surgery?is a program implementing the agent, and must output either yes or no.Destinyis either good or bad.Fortuneis always good ifSurgery?is yes, and is the same asDestinyotherwise.$is $100 ifDestinyis good and $10 otherwise, minus $10 ifSurgeryis yes. Surgery is expensive!
Now let's say that you expect even odds on whether or not your destiny is good or bad, e.g. the probability that Destiny=good is 50%.
If the Surgery? node is a program that implements causal decision theory, then that program will choose between yes and no using the following reasoning:
- The action node is
Surgery? - The available actions are yes and no
- The payoff node is
$ - Consider the action yes
- Replace the value of
Surgery?with a function that always returns yes - Calculate the value of
$ - We would get $90 if
Destiny=good - We would get $0 if
Destiny=bad - This is $45 in expectation.
- Replace the value of
- Consider the action no
- Replace the value of
Surgery?with a function that always returns no - Calculate the value of
$ - We would get $100 if
Destiny=good - We would get $10 if
Destiny=bad - This is $55 in expectation.
- Replace the value of
- Return no, as that yields the higher value of
$.
More generally, the CDT reasoning procedure works as follows:
- Identify your action node A
- Identify your available actions Acts.
- Identify your payoff node U.
- For each action a
- Set the action node A to a by replacing the value of A with a function that ignores its input and returns a
- Evaluate the expectation of U given that A=a
- Take the a with the highest associated expectation of U.
Notice how CDT evaluates counterfactuals by setting the value of its action node in a causal graph, and then calculating its payoff accordingly. Done correctly, this allows a reasoner to figure out the causal implications of taking a specific action, without getting confused by nodes like Destiny.
CDT is the academic standard decision theory. Economics, statistics, and philosophy all assume (or, indeed, define) that rational reasoners use causal decision theory to choose between available actions.
Furthermore, narrow AI systems which consider their options using this sort of causal counterfactual reasoning are implicitly acting like they use causal decision theory.
Unfortunately, causal decision theory is broken.
5
Before we dive into the problems with CDT, let's flesh it out a bit more. Game Theorists often talk about scenarios in terms of tables that list the payoffs associated with each action. This might seem a little bit like cheating, because it often takes a lot of hard work to determine what the payoff of any given action is. However, these tables will allow us to explore some simple examples of how causal reasoning works.
I will describe a variant of the classic Prisoner's Dilemma which I refer to as the token trade. There are two players in two separate rooms, one red and one green. The red player starts with the green token, and vice versa. Each must decide (in isolation, without communication) whether or not to give their token to me, in which case I will give it to the other player.
Afterwards, they may cash their token out. The red player gets $200 for cashing out the red token and $100 for the green token, and vice versa. The payoff table looks like this:
| Give | Keep | |
| Give | ( $200, $200 ) | ( $0, $300 ) |
| Keep | ( $300, $0 ) | ( $100, $100 ) |
For example, if the green player gives the red token away, and the red player keeps the green token, then the red player gets $300 while the green player gets nothing.
Now imagine a causal decision theorist facing this scenario. Their causal graph might look something like this:

Let's evaluate this using CDT. The action node is Give?, the payoff node is $. We must evaluate the expectation of $ given Give?=yes and Give?=no. This, of course, depends upon the expected value of TheirDecision.
In Game Theory, we usually assume that the opponent is also reasoning using something like causal decision theory. Then we can reason about TheirDecision given that they are doing similar reasoning about our decision and so on. This threatens to lead to infinite regress, but in fact there are some tricks you can use to guarantee at least one equilibrium. (These are the famous Nash equilibria.) This sort of reasoning requires both agents to use a modified version of the CDT procedure which we're going to ignore today. Because while most scenarios with multiple agents require more complicated reasoning, the token trade is an especially simple scenario that allows us to ignore these complications.
In the token trade, the expected value of TheirDecision doesn't matter to a CDT agent. No matter what the probability p of TheirDecision=give happens to be, the CDT agent will do the following reasoning:
- Change
Give?to be a constant function returning yes- If
TheirDecision=give then we get $200 - If
TheirDecision=keep then we get $0 - We get 200p dollars in expectation.
- If
- Change
Give?to be a constant function returning no- If
TheirDecision=give then we get $300 - If
TheirDecision=keep then we get $100 - We get 300p + 100(1-p) dollars in expectation.
- If
Obviously, 300p+100(1-p) will be larger than 200p, no matter what probability p is.
A CDT agent in the token trade must have an expectation about TheirDecision captured by a probability p that they will give their token, and we have just shown that no matter what that p is, the CDT agent will keep their token.
When something like this occurs (where Give?=no is better regardless of the value of TheirDecision) we say that Give?=no is a "dominant strategy". CDT executes this dominant strategy, and keeps its token.
6
Of course, this means that each player will get $100, when they could have both recieved $200. This may seem unsatisfactory. Both players would agree that they could do better by trading tokens. Why don't they coordinate?
The classic response is that the token trade (better known as the Prisoner's Dilemma) is a game that explicitly disallows coordination. If players do have an opportunity to coordinate (or even if they expect to play the game mulitple times) then they can (and do!) do better than this.
I won't object much here, except to note that this answer is still unsatisfactory. CDT agents fail to cooperate on a one-shot Prisoner's Dilemma. That's a bullet that causal decision theorists willingly bite, but don't forget that it's still a bullet.
7
Failure to cooperate on the one-shot Prisoner's Dilemma is not necessarily a problem. Indeed, if you ever find yourself playing a token trade against an opponent using CDT, then you had better hold on to your token, because they surely aren't going to give you theirs.
However, CDT does fail on a very similar problem where it seems insane to fail. CDT fails at the token trade even when it knows it is playing against a perfect copy of itself.
I call this the "mirror token trade", and it works as follows: first, I clone you. Then, I make you play a token trade against yourself.
In this case, your opponent is guaranteed to pick exactly the same action that you pick. (Well, mostly: the game isn't completely symmetric. If you want to nitpick, consider that instead of playing against a copy of yourself, you must write a red/green colorblind deterministic computer program which will play against a copy of itself.)
The causal graph for this game looks like this:
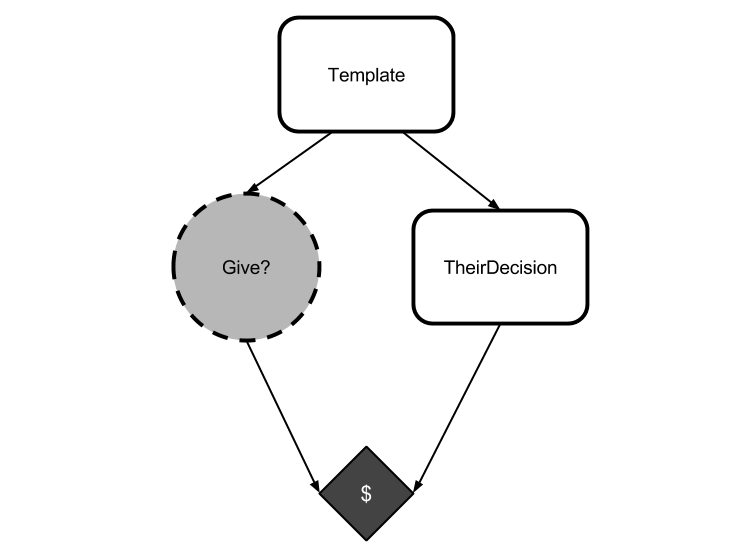
Because I've swept questions of determinism and asymmetry under the rug, both decisions will be identical. The red copy should trade its token, because that's guaranteed to get it the green token (and it's the only way to do so).
Yet CDT would have you evaluate an action by considering what happens if you replace the node Give? with a function that always returns that action. But this intervention does not affect the opponent, which reasons the same way! Just as before, a CDT agent treats TheirDecision as if it has some probability of being give that is independent from the agent's action, and reasons that "I always keep my token while they act independently" dominates "I always give my token while they act independently".
Do you see the problem here? CDT is evaluating its action by changing the value of its action node Give?, assuming that this only affects things that are caused by Give?. The agent reasons counterfactually by considering "what if Give? were a constant function that always returned yes?" while failing to note that overwriting Give? in this way neglects the fact that Give? and TheirDecision are necessarily equal.
Or, to put it another way, CDT evaluates counterfactuals assuming that all nodes uncaused by its action are independent of its action. It thinks it can change its action and only look at the downstream effects. This can break down when there are acausal connections between the nodes.
After the red agent has been created from the template, its decision no longer causally affects the decision of the green agent. But both agents will do the same thing! There is a logical connection, even though there is no causal connection. It is these logical connections that are ignored by causal counterfactual reasoning.
This is a subtle point, but an important one: the values of Give? and TheirDecision are logically connected, but CDT's method of reasoning about counterfactuals neglects this connection.
8
This is a known failure mode for causal decision theory. The mirror token trade is an example of what's known as a "Newcomblike problem".
Decision theorists occasionally dismiss Newcomblike problems as edge cases, or as scenarios specifically designed to punish agents for being "rational". I disagree.
And finally, eight sections in, I'm ready to articulate the original point: Newcomblike problems aren't a special case. They're the norm.
But this post has already run on for far too long, so that discussion will have to wait until next time.